Sayısal Çözüm Yöntemleri - Sabit Kesen Yöntemi (Regula-Falsi)

Merhabalar;

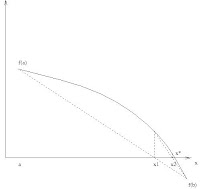
Sabit kesen yöntemi(False position method - Regula Falsi) bisection method ve secant methodun kombinasyonu şeklindedir.y=f(x) verilen [a,b] aralığında sürekli ve f(a)*f(b)<0 (yani verilen aralıkta fonksiyonun bir kökü bulunması gerekiyor.)Aralığı bisectiondan farklı olarak ağırlıklı ortalamaya bölerek adımlarımızı ilerlettiğimizde k.adımın limit durumunda bulduğumuz ağırlıklı ortalama fonksiyonun köküne eşittir.Hangi aralıkta devam etmemiz gerektiğine ise;

f(a)*f(w)<0>f(w)*f(b)<0 ise yeni aralık [w,b]

w = ( a*f(b) - b*f(a) ) / (f(b) - f(a))

Bir örnek çözelim.

Örn:f(x) = x³ - x -1 = 0 fonksiyonunun [1,2] aralığındaki kökünü bu sefer regula falsi ile bulalım.
1.Adım

f(1) = -1
f(2) = 5
w = ( 1*5 - 2*(-1) ) / ( 5 - (-1)) = 1.16667
f(w) = (1.16667)³ - 1.16667 - 1 = -0.57869
f(1.16667)*f(2)<0 yeni aralık [1.16667,2]

2.Adım

f(1.16667) = -0.57869
f(2) = 5
w = (1.16667*5 - 2*(-0.57869)) / (5-(-0.57869)) = 1.25311
f(w) = f(1.25311) = -0.28537
f(1.25311)*f(2)<0 yeni aralık [1.25311,2]

SolSınır SağSınır

1.00000 2.00000
1.16667 2.00000
1.25311 2.00000
**
**
**
1.32572 2.00000

16.adımda gelen sonuç.Fark ettiyseniz sabit kesen yöntemi kökün uzak olduğu sınır değerini sabit kalıyor. Regula-Falsi bisection methoddan daha iyi yakınsar.

Herkese kolay gelsin=)